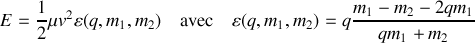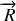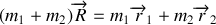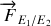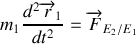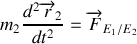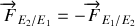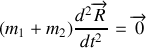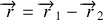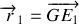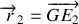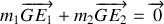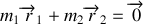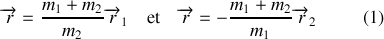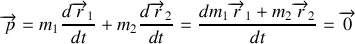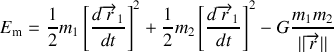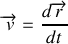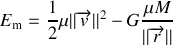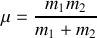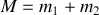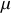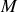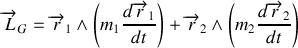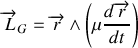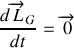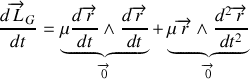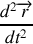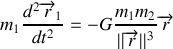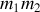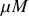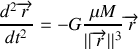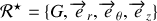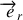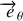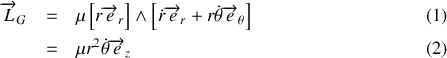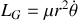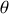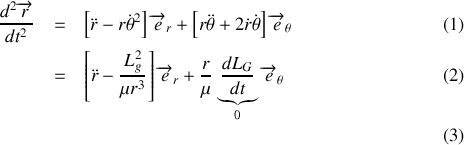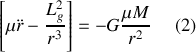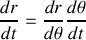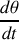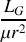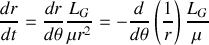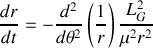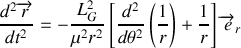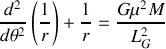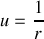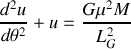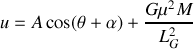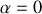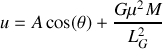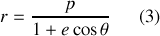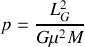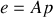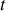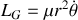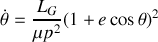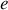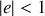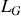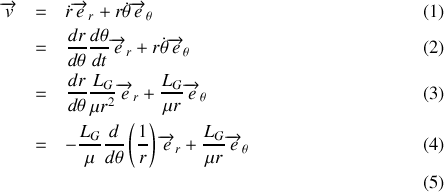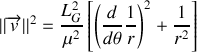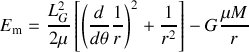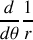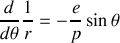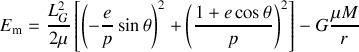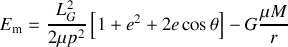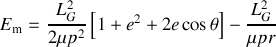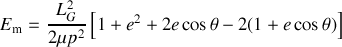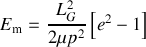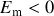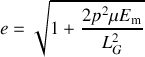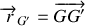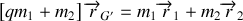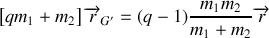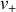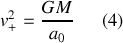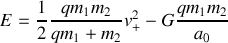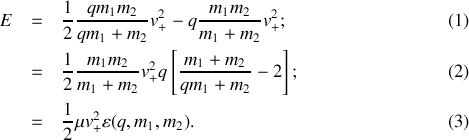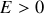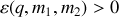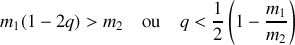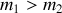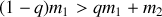1. La position
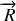 du barycentre des deux étoiles est définie par la relation vectorielle :
du barycentre des deux étoiles est définie par la relation vectorielle :
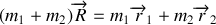 . Le référentiel barycentrique
. Le référentiel barycentrique
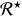 est galiléen si l'accélération du barycentre est nulle. Pour le démontrer il faut donc calculer l'accélération de chacune des étoiles. L'étoile
est galiléen si l'accélération du barycentre est nulle. Pour le démontrer il faut donc calculer l'accélération de chacune des étoiles. L'étoile
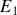 (
(
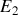 )n'est soumise qu'à l'attraction gravitationnelle de l'étoile
)n'est soumise qu'à l'attraction gravitationnelle de l'étoile
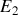 (
(
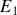 ) noté
) noté
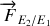 (
(
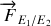 ). En appliquant une principe fondamentale de la dynamique successivement à chacune des étoiles, on obtient :
). En appliquant une principe fondamentale de la dynamique successivement à chacune des étoiles, on obtient :
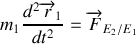
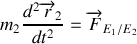
Or la loi de l'égalité de l'action et de la réaction nous permets d'affirmer que
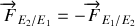 , nous avons donc
, nous avons donc
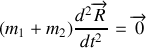
ce qui démontre bien que le barycentre se déplace avec une vitesse constante et donc que le référentiel y prenant son origine est galiléen.
2. Le vecteur position relative est définit par
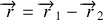 . Dans le référenciel barycentrique,
. Dans le référenciel barycentrique,
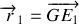 et
et
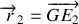 , on déduit donc de la relation de définition du barycentre
, on déduit donc de la relation de définition du barycentre
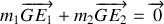 , la relation demandée
, la relation demandée
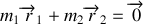 . En combinant cette relation avec la définition du vecteur position relative, on obtient deux relation définissant
. En combinant cette relation avec la définition du vecteur position relative, on obtient deux relation définissant
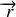 en fonction soit de
en fonction soit de
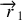 , soit de
, soit de
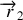 :
:
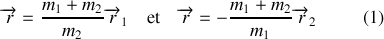
3. On voit ainsi que le vecteur position relative est proportionnel aux vecteurs position dans le repère barycentrique.
L'impulsion totale su système est la somme des impulsions de chacune de ces sous partie soit
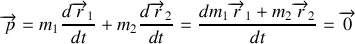 . L'impulsion totale est donc nulle.
. L'impulsion totale est donc nulle.
L'énergie mécanique est une grandeur additive, elle est composée de l'énergie cinétique de l'étoile
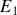 , de l'énergie cinétique de l'étoile
, de l'énergie cinétique de l'étoile
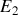 , de l'énergie d'interaction gravitationnelle entre
, de l'énergie d'interaction gravitationnelle entre
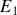 et
et
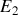 .
.
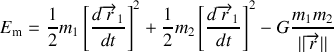
En utilisant les relations (1), les termes d'énergie cinétique s'écrivent en ne faisant apparaître que la vitesse relative
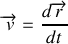 .
.
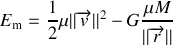
où l'on a introduit la masse réduite
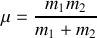 et la masse totale
et la masse totale
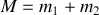 . L'énergie mécanique est similaire à celle d'un mobile fictif de masse
. L'énergie mécanique est similaire à celle d'un mobile fictif de masse
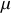 de position
de position
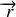 en interaction gravitationnelle avec un objet de masse
en interaction gravitationnelle avec un objet de masse
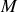 immobile à l'origine du repère. Ainsi le problème à deux corps en interaction est formellement équivalent au problème d'une particule dans un champs de force central.
immobile à l'origine du repère. Ainsi le problème à deux corps en interaction est formellement équivalent au problème d'une particule dans un champs de force central.
Le moment cinétique du système est aussi la somme des moments cinétique de chacune des sous partie soit :
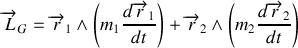
que l'on peut écrire en remplaçant
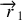 et
et
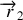 en fonction de
en fonction de
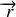 :
:
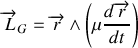
Pour démontrer que le mouvement est plan, on démontre que le moment cinétique est un vecteur constant, c'est-à-dire que
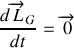 . En effectuant la dérivation à partir de l'expression précédement établie, on obtient
. En effectuant la dérivation à partir de l'expression précédement établie, on obtient
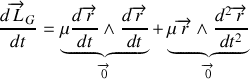
le premier terme est nul puisqu'il correspond au produit vectoriel de vecteur colinéaire, le second car l'accélération
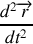 est colinéaire avec le vecteur position
est colinéaire avec le vecteur position
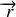 . En effet, d'après le principe fondamentale de la dynamique l'accélération est colinéaire à la somme des forces extérieurs appliquées, or ici l'unique force appliquée au mobile fictif est l'interaction gravitationnelle qui est colinéaire au vecteur position (force centrale). Ainsi le moment cinétique est un vecteur constant or il est par définition perpendiculaire au vecteur position. A chaque instant, le vecteur position est donc perpendiculaire à une droite fixe de l'espace, il est donc constamment contenue dans un même plan et donc le mouvement est plan.
. En effet, d'après le principe fondamentale de la dynamique l'accélération est colinéaire à la somme des forces extérieurs appliquées, or ici l'unique force appliquée au mobile fictif est l'interaction gravitationnelle qui est colinéaire au vecteur position (force centrale). Ainsi le moment cinétique est un vecteur constant or il est par définition perpendiculaire au vecteur position. A chaque instant, le vecteur position est donc perpendiculaire à une droite fixe de l'espace, il est donc constamment contenue dans un même plan et donc le mouvement est plan.
4. Le référentiel barycentrique
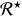 étant galiléen, on peut appliquer y le principe fondamentale de la dynamique à l'étoiles
étant galiléen, on peut appliquer y le principe fondamentale de la dynamique à l'étoiles
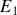 :
:
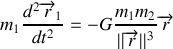
En remplaçant
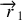 en fonction de
en fonction de
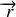 et
et
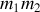 par
par
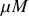 , on obtient l'expression du principe fondamentale de la dynamique pour le mobile fictif
, on obtient l'expression du principe fondamentale de la dynamique pour le mobile fictif
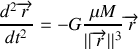
La résolution de cette équation différentielle vectorielle nécessite la projection dans un repère, il est commode de choisir un repère cylindrique :
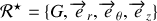 avec les axes
avec les axes
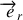 et
et
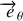 dans le plan de la trajectoire. Dans ce calcul, on va bien entendu utiliser la conservation du moment cinétique aussi est-il utile de commencer par calculer son expression dans le repère choisi :
dans le plan de la trajectoire. Dans ce calcul, on va bien entendu utiliser la conservation du moment cinétique aussi est-il utile de commencer par calculer son expression dans le repère choisi :
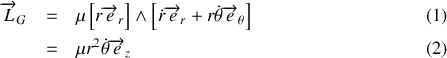
Dans la suite, on notera
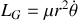 le module du moment cinétique. La conservation du moment cinétique exprime une dépendance entre la variation de
le module du moment cinétique. La conservation du moment cinétique exprime une dépendance entre la variation de
 et la variation de
et la variation de
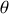 , aussi peut-on l'utiliser pour exprimer l'accélération uniquement en fonction de la dépendance radiale, en effet
, aussi peut-on l'utiliser pour exprimer l'accélération uniquement en fonction de la dépendance radiale, en effet
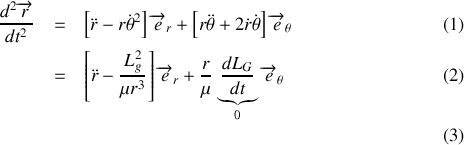
l'accélération est donc purement radiale (ce qui est cohérent avec le fait que la force le soit aussi) et ne depend que de la variable
 . L'expression vectorielle du principe fondamentale de la dynamique est donc équivalente à l'expression scalaire :
. L'expression vectorielle du principe fondamentale de la dynamique est donc équivalente à l'expression scalaire :
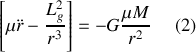
La résolution de cette équation donnera la variation temporelle du rayon
 puis en utilisant la conservation du moment cinétique, on obtiendra la variation temporelle de l'angle
puis en utilisant la conservation du moment cinétique, on obtiendra la variation temporelle de l'angle
 . Cependant il existe un moyen pour obtenir directement d'équation différentielle donnant la trajectoire.
. Cependant il existe un moyen pour obtenir directement d'équation différentielle donnant la trajectoire.
En remarquant que :
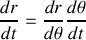 puis en remplacant
puis en remplacant
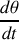 par
par
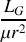 on peut écrire
on peut écrire
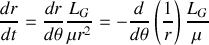 on remplace ainsi une dérivée temporelle par une dérivée angulaire. En itérant, on obtient sans peine
on remplace ainsi une dérivée temporelle par une dérivée angulaire. En itérant, on obtient sans peine
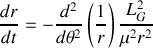 . L'accélération peut donc s'écrire
. L'accélération peut donc s'écrire
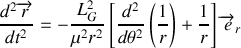
Ce résultat est connu sous l'appellation "formule de Binet'' et permet d'écrire (2) sous la forme
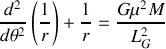
Cette relation est une équation différentielle linéaire par rapport à la variable
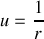 du second ordre avec second membre. En posant le changement de variable
du second ordre avec second membre. En posant le changement de variable
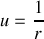 on obtient
on obtient
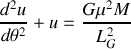
dont les solutions sont
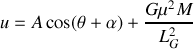 avec
avec
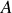 et
et
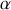 des constantes d'intégrations définies par les conditions initiales. En choisissant correctement les axes du repère, on peut toujours obtenir
des constantes d'intégrations définies par les conditions initiales. En choisissant correctement les axes du repère, on peut toujours obtenir
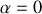 soit
soit
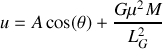 . Finalement, on obtient l'équation de la trajectoire
. Finalement, on obtient l'équation de la trajectoire
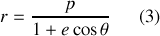
où l'on a posé
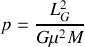 et
et
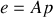
Remarquons que le connaissance de la trajectoire permet de déterminer l'équation horaire du mouvement en déterminant la position à un instant
 le long de la trajectoire ce qui nécessite un paramètre. Ici le paramètre pertinent est l'angle
le long de la trajectoire ce qui nécessite un paramètre. Ici le paramètre pertinent est l'angle
 . L'évolution temporelle de
. L'évolution temporelle de
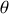 et donnée par l'équation différentielle exprimant la conservation du moment cinétique
et donnée par l'équation différentielle exprimant la conservation du moment cinétique
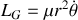 en remplaçant
en remplaçant
 en fonction de
en fonction de
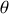 à l'aide de l'équation de la trajectoire.
à l'aide de l'équation de la trajectoire.
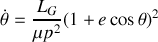
L'expression analytique de la solution de cette équation existe mais n'apporte rien de particulier ici et le calcul n'est pas reporté.
L'étoiles
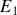 et
et
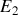 orbitent l'une autour de l'autre si la distance qui les sépare reste finie, ce qui nécessite que
orbitent l'une autour de l'autre si la distance qui les sépare reste finie, ce qui nécessite que
 reste borné par une valeur finie. On regardant l'équation de la trajectoire (3) on note que cette condition correspond à une condition sur le paramètre
reste borné par une valeur finie. On regardant l'équation de la trajectoire (3) on note que cette condition correspond à une condition sur le paramètre
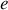 telle que
telle que
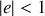 . L'équation générale de la trajectoire (3) est celle d'une conique et le paramètre
. L'équation générale de la trajectoire (3) est celle d'une conique et le paramètre
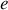 est "l'excentricité". Lorsque
est "l'excentricité". Lorsque
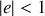 , la trajectoire est une ellipse, ce qui est correspond bien à des étoiles orbitant l'une autour de l'autre.
, la trajectoire est une ellipse, ce qui est correspond bien à des étoiles orbitant l'une autour de l'autre.
Ce résultat peut être obtenu en raisonnant sur l'énergie mécanique
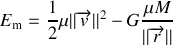
mais avant tout faisons la remarque suivante :
L'énergie mécanique est composée d'énergie cinétique qui est toujours positive et d'énergie mécanique qui est ici toujours négative. Au cours du mouvement, il y a transfert entre l'énergie cinétique et l'énergie potentiel de sorte que l'énergie mécanique soit constante. Si le système n'est pas lié, c'est-à-dire que les étoiles s'éloignent infiniment l'une de l'autre avec une vitesse relative non-nulle, alors l'énergie potentiel devient nulle et l'énergie mécanique est donc positive Inversement, si le système est lié, il existe pour une position donnée une valeur maximale de l'éloignement correspondant à une vitesse nulle (points de rebroussement), dans ce cas, l'énergie mécanique est négative.
Ainsi, du signe de l'énergie, on en déduit la nature de la trajectoire (lié ou libre).
Il est possible d'exprimer autrement la condition sur l'excentricité à partir de l'expression de l'énergie mécanique. Pour cela, il faut exprimer la vitesse en fonction de la variable angulaire
 et du module du moment cinétique
et du module du moment cinétique
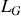 . En utilisant de nouveau un repère cylindrique, on obtient l'expression de la vitesse
. En utilisant de nouveau un repère cylindrique, on obtient l'expression de la vitesse
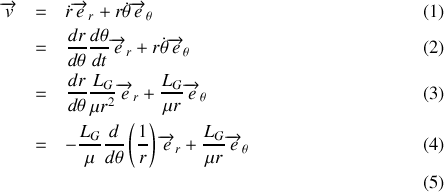
d'où en déduit l'expression de la norme au carré de la vitesse :
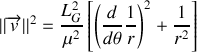
et donc de l'énergie mécanique :
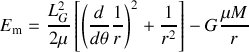
La dérivée
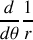 se calcule en utilisant l'équation de la trajectoire (3) :
se calcule en utilisant l'équation de la trajectoire (3) :
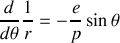 soit en substituant
soit en substituant
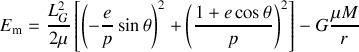 ,
,
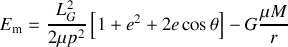 .
.
La relation de définition du paramètre
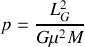 permets de ré-écrire l'énergie mécanique sous la forme :
permets de ré-écrire l'énergie mécanique sous la forme :
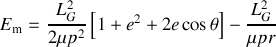 ,
,
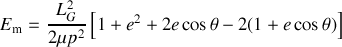 ,
,
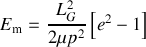 .
.
On sait que l'existence de trajectoire liée impose
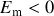 , ce qui correspond bien à
, ce qui correspond bien à
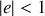 , condition établi à partir de l'expression de la trajectoire. Au passage, on obtient une nouvelle définition de l'excentricité
, condition établi à partir de l'expression de la trajectoire. Au passage, on obtient une nouvelle définition de l'excentricité
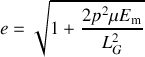
en fonction des constantes du mouvement: énergie mécanique et moment cinétique.
5. Centre de gravité après l'explosion
Après l'explosion, la position du nouveau centre de gravié
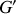 est défini en fonction de l'ancien centre
est défini en fonction de l'ancien centre
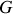 par le vecteur position
par le vecteur position
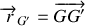 . La définition du centre de gravité donne la relation
. La définition du centre de gravité donne la relation
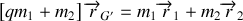 .
.
En utilisant les relations (1) on obtient l'expression de la position du nouveau de gravité en fonction de la position relative :
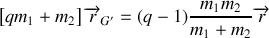 .
.
6. Energie après explosion
Avant l'explosion, la trajectoire du mobile réduit est circulaire de rayon
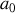 . La vitesse n'étant pas modifiée pendant l'explosion, on déduit aisément le module
. La vitesse n'étant pas modifiée pendant l'explosion, on déduit aisément le module
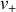 de la vitesse juste après l'explosion :
de la vitesse juste après l'explosion :
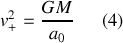
L'explosion entraînant une perte de masse, il n'y a pas bien évidement conservation de l'énergie. Cependant, on peut calculer l'énergie juste après l'explosion sous la forme suivante :
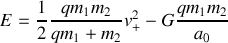
L'expression (4) permet de faire apparaître le module de la vitesse dans le terme d'énergie potentielle et de retrouver la forme demandée :
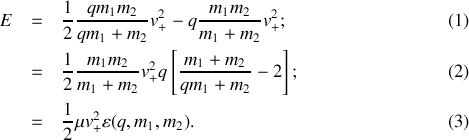
On a démontrer précédemment que les trajectoire liés correspondent à des valeurs négatives de l'énergie. En conséquence, on peut affirmer que l'explosion brise le lien gravitationnel si
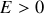 ce qui est équivalent à
ce qui est équivalent à
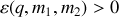 soit
soit
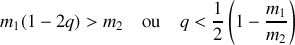
Il est immédiat que ceci ne peut se produire que si l'étoile ayant explosé est la plus massive des deux (
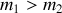 ). Il faut alors que l'étoile massive perdent au minimum 50% de sa masse.
). Il faut alors que l'étoile massive perdent au minimum 50% de sa masse.
Un autre critère équivalent peut être obtenu en notant que
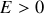 implique
implique
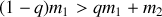 . La masse perdue par l'explosion doit ainsi être supérieure à la masse restante pour qu'il y ait brisure à long terme du lien gravitationnel (c'est à dire des trajectoires de type parabolique ).
. La masse perdue par l'explosion doit ainsi être supérieure à la masse restante pour qu'il y ait brisure à long terme du lien gravitationnel (c'est à dire des trajectoires de type parabolique ).
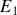 et
et
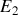 de masse respective
de masse respective
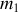 et
et
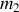 en interaction gravitationnelle. On suppose que les étoiles forment un système isolé et que l'on peut les assimiler à des points matériels.
en interaction gravitationnelle. On suppose que les étoiles forment un système isolé et que l'on peut les assimiler à des points matériels.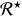 ayant pour origine le barycentre
ayant pour origine le barycentre
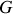 des deux étoiles est un référentiel galiléen.
des deux étoiles est un référentiel galiléen.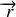 des deux étoiles en fonction des vecteurs position
des deux étoiles en fonction des vecteurs position
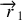 et
et
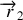 de chacune des étoiles. Quelle est la relation entre
de chacune des étoiles. Quelle est la relation entre
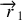 et
et
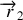 dans le référentiel
dans le référentiel
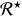
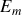 , l'impulsion
, l'impulsion
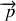 et le moment cinétique
et le moment cinétique
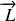 du système dans le référentiel
du système dans le référentiel
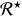 en fonction de la position relative, de la vitesse relative et des paramètres du système. En déduire que le mouvement des deux étoiles est contenue dans un plan.
en fonction de la position relative, de la vitesse relative et des paramètres du système. En déduire que le mouvement des deux étoiles est contenue dans un plan. et donner l'équation de la trajectoire en coordonnée polaire (vous pouvez utiliser les résultats relatifs aux mouvement dans un champs de force centrale).
et donner l'équation de la trajectoire en coordonnée polaire (vous pouvez utiliser les résultats relatifs aux mouvement dans un champs de force centrale).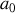 , la vitesse relative
, la vitesse relative
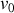 , l'énergie mécanique
, l'énergie mécanique
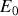 et la masse réduite
et la masse réduite
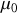 . L'étoile
. L'étoile
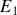 explose instantanément en supernova et éjecte une fraction
explose instantanément en supernova et éjecte une fraction
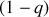 de masse de sorte que sa masse finale vaut
de masse de sorte que sa masse finale vaut
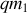 avec
avec
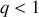 . L'éjection de matière est isotrope et ne modifie pas la vitesse de
. L'éjection de matière est isotrope et ne modifie pas la vitesse de
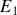 . On suppose enfin que l'étoile
. On suppose enfin que l'étoile
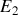 n'est pas affectée par l'explosion.
n'est pas affectée par l'explosion.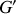 après l'explosion.
après l'explosion.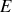 après l'explosion. Montrer qu'elle peut se mettre sous la forme :
après l'explosion. Montrer qu'elle peut se mettre sous la forme :