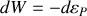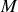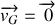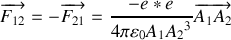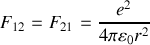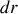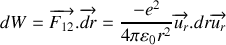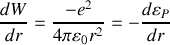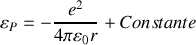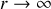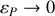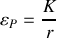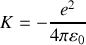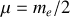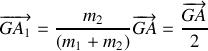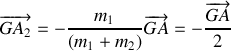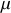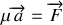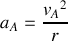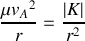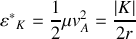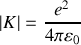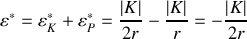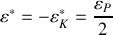Énoncé
Le positronium est un atome constitué d'un électron
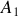 (de masse
(de masse
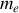 et de charge
et de charge
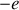 ) en interaction avec un positron
) en interaction avec un positron
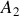 , antiparticule de l'électron (de masse
, antiparticule de l'électron (de masse
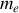 et de charge
et de charge
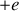 ). On désigne par
). On désigne par
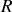 le référentiel du laboratoire que l'on peut considéré comme isolé. Du fait des faibles masses, on négligera l'effet de la pesanteur dans tout le problème.
le référentiel du laboratoire que l'on peut considéré comme isolé. Du fait des faibles masses, on négligera l'effet de la pesanteur dans tout le problème.
Définir le référentiel du centre de masse
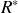 associé à ce système. Ce référentiel est-il galiléen ?
associé à ce système. Ce référentiel est-il galiléen ?Montrer que l'énergie potentielle d'interaction électrostatique entre
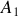 et
et
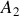 s'exprime comme
s'exprime comme
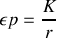 ,
,
 étant la distance entre les 2 charges et
étant la distance entre les 2 charges et
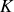 une constante que l'on explicitera en fonction des données de l'énoncé.
une constante que l'on explicitera en fonction des données de l'énoncé.Dans
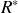 , les mouvements de
, les mouvements de
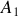 et
et
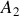 s'obtiennent à partir de celui d'une seule particule fictive
s'obtiennent à partir de celui d'une seule particule fictive
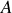 soumise à la force d'interaction.
soumise à la force d'interaction.a) Quelle est la masse de
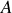 ? Pourquoi le mouvement de
? Pourquoi le mouvement de
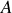 est-il plan ?
est-il plan ?b) Comment déduit-on les mouvements de
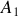 et
et
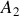 dans
dans
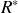 de celui de
de celui de
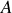 dans
dans
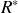 .
.La particule
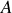 a un mouvement circulaire uniforme autour du centre de masse
a un mouvement circulaire uniforme autour du centre de masse
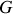 .
.a) Etablir l'expression de l'énergie cinétique du système dans
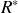
b) En déduire l'énergie totale du positronium dans le référentiel
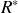 .
. c) Sachant que toute particule accélérée rayonne de l'énergie sous forme électromagnétique, comment varient
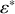 ,
,
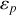 et
et
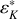 ?
?