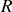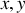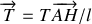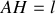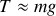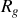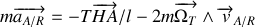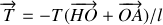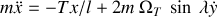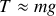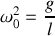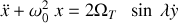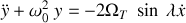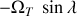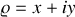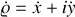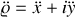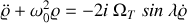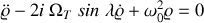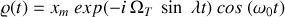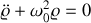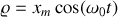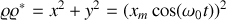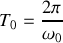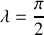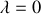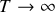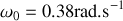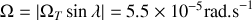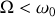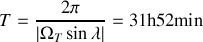En 1851, le physicien francais Foucault a observé le mouvement d'un pendule supposé simple, destiné à prouver la rotation de la Terre. Foucault a étudié le phénomène tout d'abord avec une masse de 5 kg suspendue a un fil de 2 m de long, puis à l'Observatoire de Paris avec un pendule de 11 m et enfin de façon spectaculaire au Panthéon à Paris (latitude 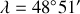) avec une masse de 28 kg suspendue à la coupole par un fil d'acier de 1,4 mm de diamètre et de longueur l = 67 m.

Figure 1

Un point 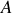de masse 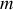est suspendu par l'intermediaire d'un fil sans masse de longueur 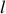à un point 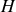fixe par rapport au sol. On reconnait la description d'un pendule simple (de pulsation 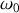) : observé dans de bonnes conditions, ce pendule peut être qualifié de pendule de Foucault.

1. Soit 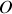le point d'équilibre du pendule. Pour des oscillations de faible amplitude, le mouvement est quasi plan et s'effectue pratiquement dans le plan horizontal 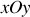. Montrer que ceci implique que la tension 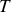du fil est confondue avec le poids de la masse 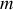. On écarte le pendule de cette position d'équilibre 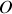en un point de coordonnées 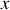et 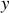(très inférieures à 1). Montrer que le pendule sera soumis à la tension du fil d'expression:

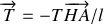
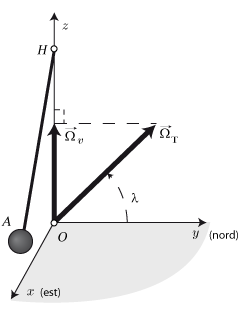
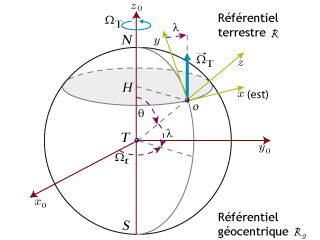
2. Ecrire les équations du mouvement dans le plan, tenant compte du fait que le référentiel terrestre est non galiléen.

   On posera 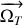la vitesse de rotation de la terre autour de son axe. Montrer au final que les équations du mouvement sont les suivantes :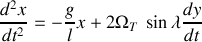

   

   et

   

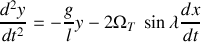
3. Intégrer les équations du mouvement en posant 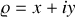, ce qui revient à repérer le point 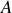du plan par le nombre complexe 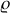. Montrer que l'on arrive à une équation différentielle linéaire à coefficients constants.

4. Trouver les solutions 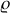de l'équation précédente en fonction de 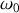, , 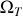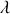et des conditions initiales: 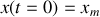, 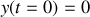et

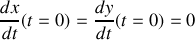
5. En supposant que la Terre ne tourne pas ( 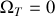). Montrer que le point 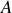décrit une ellipse avec une période 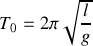. Montrer que l'existence de la rotation de la Terre implique que l'ellipse-trajectoire du point 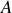tourne autour de l'axe vertical 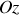par rapport aux axes fixés au sol avec la vitesse angulaire .

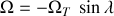   Que se passe t-il aux pôles ou à l'équateur ?

6. Avec les valeurs de l' expérience du Panthéon à Paris, calculer les valeurs de 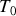et . En déduire la valeur de la période de rotation complète de l'ellipse.