Énoncé
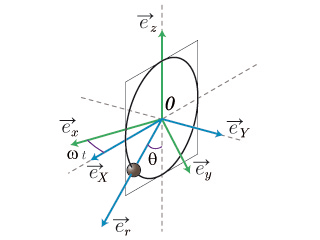
Une perle
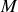 de masse
de masse
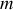 (en bleue sur la figure) glisse sans frottement sur une circonférence de centre
(en bleue sur la figure) glisse sans frottement sur une circonférence de centre
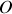 de rayon
de rayon
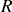 placée dans le plan vertical. La circonférence peut tourner autour de son diamètre vertical par rapport au référentiel
placée dans le plan vertical. La circonférence peut tourner autour de son diamètre vertical par rapport au référentiel
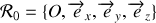 du laboratoire considéré comme galiléen (
du laboratoire considéré comme galiléen (
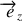 a la direction de la verticale ascendante). A l'instant initial, la perle est à l'équilibre et la circonférence est mise en rotation avec une vitesse angulaire
a la direction de la verticale ascendante). A l'instant initial, la perle est à l'équilibre et la circonférence est mise en rotation avec une vitesse angulaire
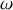 constante autour de son diamètre vertical.
constante autour de son diamètre vertical.
En utilisant un référentiel
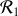 lié à la circonférence, déterminer l'équation du mouvement, la position de la perle sur la circonférence étant repérée par l'angle
lié à la circonférence, déterminer l'équation du mouvement, la position de la perle sur la circonférence étant repérée par l'angle
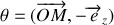 .
.En déduire les positions d'équilibre de la perle et discuter de leurs stabilités en fonction du paramètre
 .
.Déterminer, au point d'équilibre, les forces de contact du cerceau sur la perle.
1. Pour déterminer l'équation du mouvement :
a) Exprimer le vecteur position de la perle dans le repère polaire
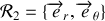 lié à la circonférence puis dans le repère cartésien
lié à la circonférence puis dans le repère cartésien
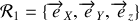 lié à la circonférence et enfin dans le repère
lié à la circonférence et enfin dans le repère
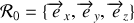 lié au sol.
lié au sol.
b) Exprimer les composantes de l'accélération de la perle par rapport au référentiel galliléen
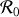 dans le repère cartésien
dans le repère cartésien
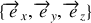 , puis dans le repère sphérique
, puis dans le repère sphérique
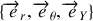 .
.
c) Identifier les composantes de l'accélération de la perle par rapport au référentiel
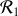 lié à la circonférence.
lié à la circonférence.
d) En déduire les forces d'inertie dans le référentiel
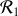 .
.
2. Pour déterminer la stabilité des positions d'équilibre :
a) Identifier les positions d'équilibre
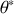 en cherchant les solutions de l'équation du mouvement pour une vitesse et une accélération nulles.
en cherchant les solutions de l'équation du mouvement pour une vitesse et une accélération nulles.
b) Faire un changement de variable en posant
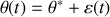 et obtenir l'équation du mouvement pour la variable
et obtenir l'équation du mouvement pour la variable
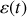 .
.
Quelle doit être la condition sur le comportement asymptotique de
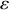 (c'est-à-dire la
(c'est-à-dire la
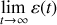 ) pour un point d'équilibre stable ?
) pour un point d'équilibre stable ?
c) Résoudre cette équation en supposant
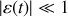 . Déduire de la stabilité de
. Déduire de la stabilité de
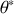 en fonction du comportement asymptotique de
en fonction du comportement asymptotique de
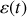 .
.
1. Equation du mouvement dans le référentiel
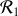
a) Coordonnées du vecteur position dans les différents repères
Les coordonnées cartésiennes du vecteur position
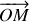 s'expriment le plus simplement dans le repère polaire lié à la circonférence
s'expriment le plus simplement dans le repère polaire lié à la circonférence
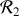 :
:
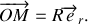
Sa décomposition dans le repère cartésien tournant se déduit par la projection de
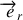 sur les axes
sur les axes
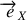 et
et
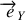 , de manière générale,
, de manière générale,
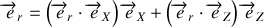
puisque le repère est orthogonal (
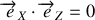 ). Les vecteurs de base d'un repère étant choisis unitaires, les produits scalaires sont simplement
). Les vecteurs de base d'un repère étant choisis unitaires, les produits scalaires sont simplement
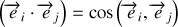 où
où
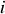 et
et
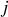 représentent des indices quelconques.
représentent des indices quelconques.
Tous calculs effectués, on obtient :
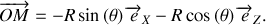
Pour obtenir la décomposition dans le repère
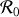 , il faut à nouveau projeter les vecteurs de base du repère
, il faut à nouveau projeter les vecteurs de base du repère
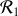 dans le repère
dans le repère
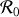 .
.
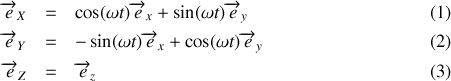
Comme précédemment, la composante du vecteur
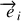 dans la direction
dans la direction
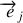 est le produit scalaire des deux vecteurs c'est-à-dire
est le produit scalaire des deux vecteurs c'est-à-dire
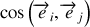 . La décomposition du vecteur position dans le repère
. La décomposition du vecteur position dans le repère
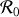 est ici
est ici
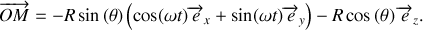
Nous avons ainsi établi tous les ingrédients pour effectuer simplement le passage d'un repère à un autre. Les calculs suivants pourront donc être menés dans le repère le plus commode.
b) Coordonnées de l'accélération de la perle par rapport au référentiel
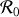 :
:
L'accélération de la perle par rapport au référentiel
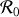 s'obtient en dérivant deux fois le vecteur position
s'obtient en dérivant deux fois le vecteur position
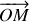 , en considérant les vecteurs de base du repère
, en considérant les vecteurs de base du repère
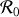 comme fixes. La première dérivation fournit la vitesse
comme fixes. La première dérivation fournit la vitesse
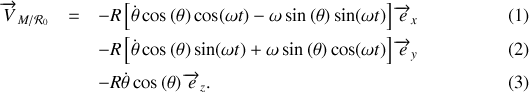
qui s'écrit de manière beaucoup plus élégante dans le repère sphérique
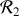 :
:
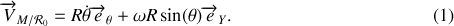
Le calcul de la vitesse peut se faire de manière plus directe en introduisant le vecteur rotation
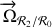 du repère
du repère
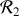 par rapport à
par rapport à
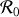 . Cette rotation est la composition de deux rotations : celle qui amène
. Cette rotation est la composition de deux rotations : celle qui amène
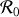 en coïncidence avec
en coïncidence avec
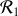 puis celle qui amène
puis celle qui amène
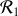 en coïncidence avec
en coïncidence avec
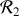 . On peut formaliser cela de la manière suivante :
. On peut formaliser cela de la manière suivante :
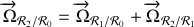
Or comme il est aisé de le voir
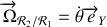 et
et
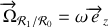 . Le vecteur de rotation ainsi défini, nous pouvons utiliser la règle de changement de repère
. Le vecteur de rotation ainsi défini, nous pouvons utiliser la règle de changement de repère
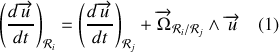
soit ici
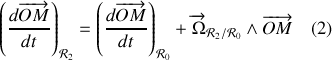
Dans l'expression (2), le terme du membre de gauche est la vitesse de la perle par rapport au référentiel
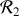 , qui se calcule en dérivant l'expression du vecteur position
, qui se calcule en dérivant l'expression du vecteur position
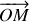 en supposant fixes les vecteurs de base du repère associé au référentiel
en supposant fixes les vecteurs de base du repère associé au référentiel
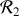 :
:
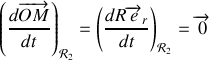
puisque
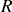 et
et
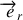 sont constants.
sont constants.
Le premier terme du membre de droite de (2) est la vitesse de la perle dans le référentiel galiléen
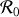 . On trouve finalement la vitesse recherchée sous la forme
. On trouve finalement la vitesse recherchée sous la forme
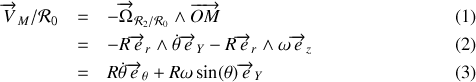
Le calcul de l'accélération, bien qu'un peu long, n'est pas compliqué,
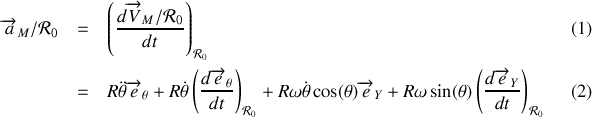
Il fait intervenir la dérivée de deux vecteurs tournants que l'on calcule aisément à l'aide de l'expression (1). La première dérivée vaut
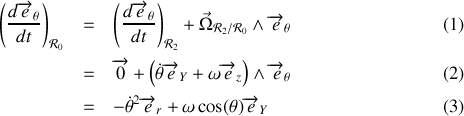
où on a utilisé les relations
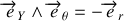 et
et
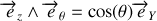 ; quant à la seconde,
; quant à la seconde,
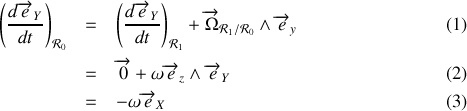
Finalement, l'accélération de
 par rapport au référentiel
par rapport au référentiel
 vaut :
vaut :
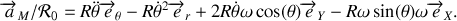
c) Accélération de la perle par rapport au référentiel tournant
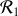 :
:
La vitesse du point
 par rapport au référentiel tournant s'exprime le plus simplement dans le repère
par rapport au référentiel tournant s'exprime le plus simplement dans le repère
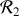 .
.
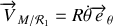
Il en est de même pour l'accélération
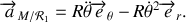
On remarque ainsi que
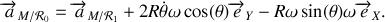
Lors de l'application du principe fondamental de la dynamique dans le repère tournant non-galiléen
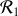 il faut donc tenir compte de la force d'inertie
il faut donc tenir compte de la force d'inertie
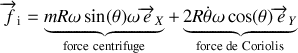
composée d'un terme centrifuge et d'un terme de Coriolis.
Application du principe fondamental de la dynamique dans le référentiel
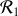
Dans le référentiel non-galiléen
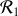 la masse
la masse
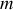 est soumise à trois forces :
est soumise à trois forces :
son poids
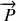 qui est vertical descendant de module
qui est vertical descendant de module
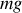
la réaction de la circonférence sur la perle
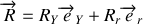
La force d'inertie
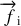
Le principe fondamental de la dynamique nous permet d'écrire l'égalité vectorielle
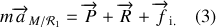
En projetant cette égalité sur les trois vecteurs de base du repère
 on obtient trois égalités scalaires :
on obtient trois égalités scalaires :
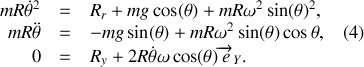
Seule l'équation (4) issue de la projection de (3) dans la direction
 est l'équation du mouvement (c'est-à-dire une équation différentielle du deuxième ordre), les deux autres équations permettant de déterminer les composantes de la réaction de la circonférence sur la perle.
est l'équation du mouvement (c'est-à-dire une équation différentielle du deuxième ordre), les deux autres équations permettant de déterminer les composantes de la réaction de la circonférence sur la perle.
2. Positions d'équilibres
a) Les positions d'équilibre sont les valeurs de
 pour lesquelles la vitesse et l'accélération de la perle sont nulles. En utilisant l'équation du mouvement (4), on déduit que les positions d'équilibre sont telles que
pour lesquelles la vitesse et l'accélération de la perle sont nulles. En utilisant l'équation du mouvement (4), on déduit que les positions d'équilibre sont telles que
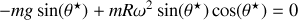
c'est-à-dire, soit
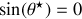 soit
soit
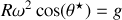 . De la première condition il vient
. De la première condition il vient
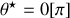 . La seconde condition n'a de solution que pour les fréquences de rotation
. La seconde condition n'a de solution que pour les fréquences de rotation
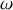 élevées, plus précisément si
élevées, plus précisément si
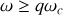 avec
avec
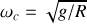 .
.
Le système mécanique possède donc deux positions d'équilibre pour les basses fréquences (
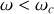 ) et quatre pour les hautes fréquences (
) et quatre pour les hautes fréquences (
 ). Toutes ces positions ne correspondent pas à des équilibres stables, il faut donc étudier la stabilité de chacune d'entres elles.
). Toutes ces positions ne correspondent pas à des équilibres stables, il faut donc étudier la stabilité de chacune d'entres elles.
b) Stabilité des positions d'équilibre
Pour étudier la stabilité d'une position d'équilibre, il faut linéariser l'équation du mouvement autour de la position d'équilibre. On obtient ainsi une équation du mouvement approchée pour le voisinage de la position d'équilibre ; cette équation étant linéaire, on peut la résoudre et ainsi déterminer le devenir d'une faible perturbation autour de la position d'équilibre. Si celle-ci croît au cours du temps, alors le point d'équilibre est instable.
Pour linéariser l'équation du mouvement (4) autour de cette position d'équilibre, on pose
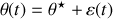 soit, en substituant,
soit, en substituant,
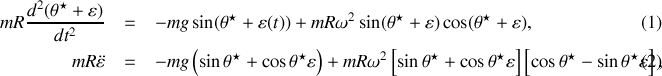
soit en linéarisant (en négligeant les termes en
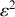 ) et en utilisant le fait que
) et en utilisant le fait que
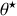 soit un point d'équilibre
soit un point d'équilibre
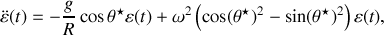
ce que l'on peut ré-écrire en utilisant la définition de
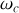 :
:
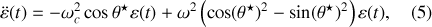
c) L'équation (5) caractérise la stabilité des positions d'équilibre.
Stabilité de
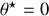 :
:
En reportant la valeur
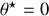 dans l'équation linéarisée (5), on obtient
dans l'équation linéarisée (5), on obtient
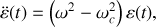
En posant
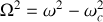 la solution de l'équation linéarisée est
la solution de l'équation linéarisée est
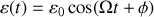 si
si
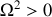 c'est-à-dire si
c'est-à-dire si
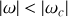 ; le mouvement est alors une oscillation d'amplitude constante traduisant un point d'équilibre stable.
; le mouvement est alors une oscillation d'amplitude constante traduisant un point d'équilibre stable. si
si
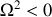 c'est-à-dire si
c'est-à-dire si
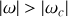 ; le mouvement s'écarte indéfiniment du point d'équilibre, il s'agit donc d'un point d'équilibre instable.
; le mouvement s'écarte indéfiniment du point d'équilibre, il s'agit donc d'un point d'équilibre instable.
Dans ce qui précède,
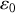 et
et
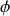 sont des constantes déterminées par les conditions initiales. Nous remarquons que le point stable caractérisé par
sont des constantes déterminées par les conditions initiales. Nous remarquons que le point stable caractérisé par
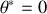 "perd'' sa stabilité lorsque la fréquence de rotation dépasse la fréquence critique
"perd'' sa stabilité lorsque la fréquence de rotation dépasse la fréquence critique
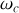 . La perle initialement au repos en
. La perle initialement au repos en
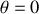 lorsque
lorsque
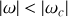 se met en mouvement dès que
se met en mouvement dès que
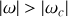 .
.
Stabilité de
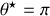 :
:
En reportant la valeur
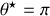 dans l'équation linéarisée (5), on obtient
dans l'équation linéarisée (5), on obtient
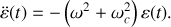
En posant
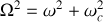 la solution de l'équation linéarisée est
la solution de l'équation linéarisée est
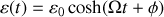 quel que soit
quel que soit
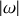 ; le mouvement s'écarte indéfiniment du point d'équilibre. Le point d'équilibre
; le mouvement s'écarte indéfiniment du point d'équilibre. Le point d'équilibre
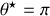 est donc toujours instable.
est donc toujours instable.
Stabilité du point défini par
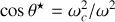
En remplaçant
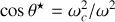 et
et
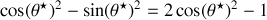 dans l'équation linéarisée (5), on obtient
dans l'équation linéarisée (5), on obtient
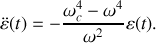
On a toujours
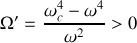 puisque sinon le point n'est pas un point d'équilibre. La solution est donc de la forme
puisque sinon le point n'est pas un point d'équilibre. La solution est donc de la forme
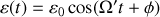 avec
avec
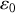 et
et
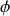 des constantes déterminées par les conditions initiales. Le point d'équilibre est donc stable puisque le mouvement est une oscillation d'amplitude constante autour du point d'équilibre.
des constantes déterminées par les conditions initiales. Le point d'équilibre est donc stable puisque le mouvement est une oscillation d'amplitude constante autour du point d'équilibre.
Remarquons que ce point d'équilibre est en fait double :
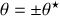 , l'égalité
, l'égalité
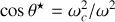 définissant deux points d'équilibre symétriques par rapport à l'axe
définissant deux points d'équilibre symétriques par rapport à l'axe
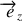 . Lorsque
. Lorsque
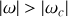 le point
le point
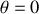 perd sa stabilité et la perle se dirige vers l'un des nouveaux points d'équilibre definis par
perd sa stabilité et la perle se dirige vers l'un des nouveaux points d'équilibre definis par
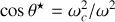 .
.
Le fait est que la perle a "le choix'' entre deux points d'équilibre. Ce sont les fluctuations du système qui orientent la perle soit à gauche, soit à droite de l'ancienne position d'équilibre
 , un peu comme une bille au sommet d'une crète peut tomber d'un côté ou de l'autre en fonction des fluctuations.
, un peu comme une bille au sommet d'une crète peut tomber d'un côté ou de l'autre en fonction des fluctuations.
Remarque :
Cet exercice présente un exemple mécanique de variation de la stabilité d'un équilibre lors de la variation d'un paramètre (ici la fréquence de rotation du cerceau). Ce comportement est général en physique et se retrouve fréquemment lors de l'étude des systèmes dynamiques et des transitions de phase des matériaux.



