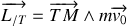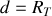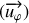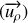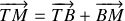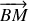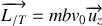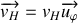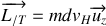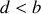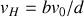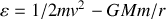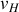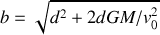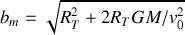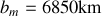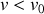Énoncé
Très loin de la Terre, une météorite
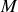de masse
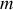a une vitesse portée par un axe situé à une distance
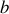du centre
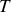de la Terre. A l'approche de notre planète, la trajectoire de cette météorite est soumise au champ gravitationnel terrestre.
Elle passe, au point
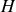, à une distance minimale de
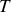, notée
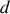. On supposera que la Terre reste immobile dans un référentiel d'inertie.
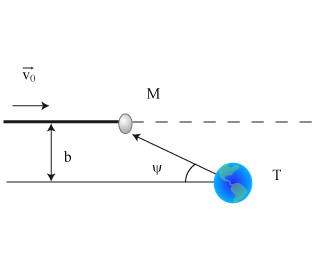
Montrer que le mouvement de la météorite est plan et faire la figure correspondant au mouvement ci-dessus.
Déterminer le module
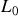du moment cinétique de la météorite par rapport à
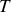, très loin de la Terre, en fonction de
,
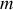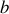et
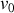. N.B. : il sera utile de décomposer le vecteur
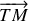en ses deux composantes, respectivement parallèle et perpendiculaire à
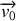.Montrer que lorsque la météorite passe en
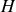sa vitesse
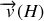est perpendiculaire à
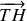. En déduire
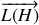en fonction de
,
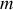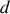et
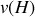.Exprimer
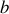en fonction de
,
,
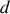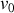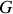(constante de la gravitation universelle),
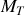(masse de la Terre).Pour
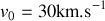, calculer la valeur
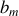de
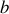en dessous de laquelle la météorite rentrera en contact avec l'atmosphère. On donne :
,
,
,
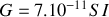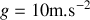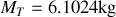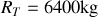(rayon de la Terre) sans tenir compte de l'atmosphère.Lorsque
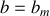calculé précédemment, qu'arrivera-t-il à des météorites ayant des vitesses initiales
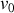, inférieures ou supérieures à
?
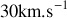