Théorème du centre d'inertie
Les forces mises en jeu sont, outre le poids, la réaction du support qui se décompose en deux : parallèlement au plan pour permettre le roulement et perpendiculairement au plan incliné en réaction, notamment au poids.
La dérivée du vecteur vitesse du centre d'inertie donne directement :
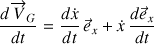
La direction
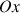, représentée par son vecteur unitaire, est fixe : le second terme ne donne aucune contribution.
En résumé, avec le bilan des forces, les équations du mouvement déduites du théorème du centre d'inertie sont :
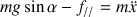
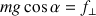
Trois inconnues (les deux composantes de la réaction du plan et l'accélération linéaire) pour deux équations, la résolution complète nécessite une équation supplémentaire qui provient du théorème du moment cinétique.
La projection sur l'axe
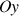exprime une contrainte de type rectiligne, puisque le mouvement du CDM est parallèle à la droite de pente. Cette équation est à comparer à la contrainte sphérique produite par un mouvement sur une sphère (exercice de l'igloo).
