Le théorème du moment cinétique
Au vu de la méthode de résolution choisie, les forces de contact doivent être présentes.
Le centre d'application de ce dernier théorème qui met en jeu la réaction du support est le CDM.
En effet :
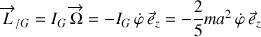
Le signe "moins" indique un vecteur rentrant par rapport au plan de la figure et une rotation de sens opposé à la trigonométrie.
Le moment de force à l'origine de la rotation s'écrit :
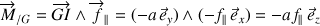
Le théorème du moment cinétique permet de déduire directement la force de contact en fonction de l'accélération angulaire :
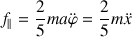
Cette relation est reportée dans les équations du théorème du centre d'inertie.
Elle permet la mise en place d'une correction de type ‘moment d'inertie d'Huygens' et de retrouver l'accélération du CDM.
L'expression de la réaction normale est également obtenue.
Cet exercice caractérise un cas de mouvement parfait du solide :
- sans glissement au point de contact, ce qui suppose une adhérence totale,
- ni de frottement de l'air et autres ralentissements au mouvement de rotation.





