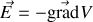On peut facilement résumer le sens de variation du champ 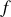en introduisant un vecteur 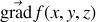dit gradient de la fonction et tel que

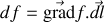
avec 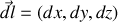l'élément de longueur au point .

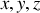Ainsi 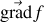a pour coordonnées

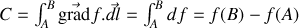
Remarquons que la "flèche du gradient" nous donne le sens de variation de la fonction 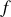, à l'opposé des puits de potentiel par exemple

Figure 10: Exemple de cuvette de potentiel et du gradient correspondant

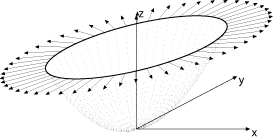
Remarquons également que si nous calculons la circulation 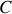du gradient le long d'une courbe 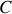entre deux points 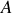et 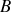nous trouvons

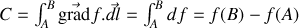
résultat à rapprocher de celui obtenu en mécanique sur le travail d'une force conservative (dérivant d'un potentiel). Ainsi la gravité dérive du potentiel 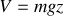par 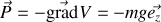et "pointe vers le bas" 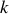 ;son travail ne dépend pas du chemin parcouru.

De même pour le champ électrique qui dérive du potentiel selon