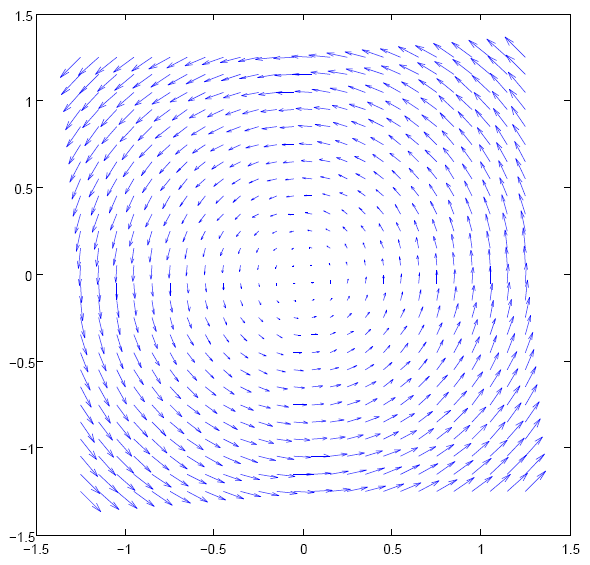
Dans le paragraphe précédent, nous n'avons envisagé que les dérivées partielles de chaque composante du champ par rapport à la variable d'espace correspondante.
Ceci dit chacune des composantes du champ vectoriel constitue un champ scalaire et a "parfaitement le droit" de dépendre des autres coordonnées ; par exemple
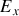peut dépendre de
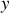et de
.
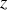L'opérateur rotationnel va nous permettre d'exploiter ces variations non prises en compte dans la divergence.
Ainsi on associe à un champ vectoriel
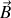(typiquement le champ magnétique) un nouveau champ vectoriel appelé rotationnel de
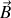et défini par
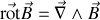
où
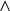dénote le produit vectoriel.
Remarquons que le rotationnel va donc dépendre de l'orientation de l'espace choisie ("règle de la main droite" ou non). Nous reviendrons sur ce point qui a d'importantes conséquences.
Le rotationnel comme son nom l'indique nous permettra de savoir à quel endroit le champ tourne autour d'une de ses sources. Ainsi le champ magnétique tournoie autour des courants localisés, à l'endroit desquels son rotationnel est non nul, et en mécanique des fluides une tornade présente des vitesses qui tournent autour de leur source.
