Ainsi, si nous considérons un champ vectoriel tridimensionnel 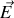(typiquement, le champ électrique ou le champ magnétique) nous pouvons calculer une quantité appelée divergence du champ définie par

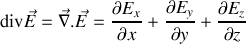
La divergence comme son nom l'indique nous permettra de savoir, si elle est non nulle, à quel endroit le champ "diverge" : par exemple, le champ électrique créé par une charge localisée n'a une divergence non nulle que dans la région de l'espace occupée par la charge.

En mécanique des fluides, cela correspondrait par exemple à un point d'injection de fluide.

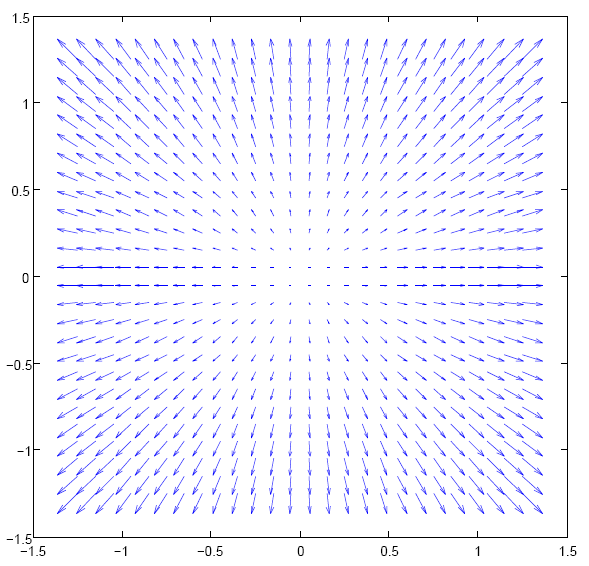
Figure 11: Cartographie bidimensionnelle du champ créé par une charge localisée; la divergence est non nulle dans la région occupée par la charge